Solve stepper systems of 2 linear equations with 2 unknowns by the methods of substitution, equalization and reduction.
The coefficients of the system can be integers , fractions and decimals , for example numbers : 3, -5, 2/7, 8.23 , etc .
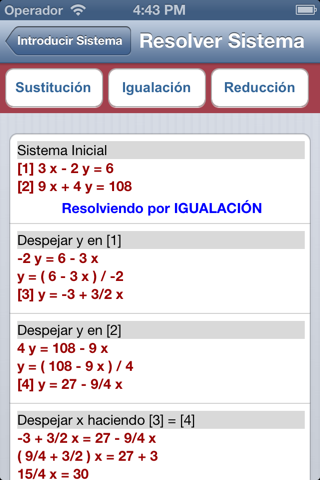
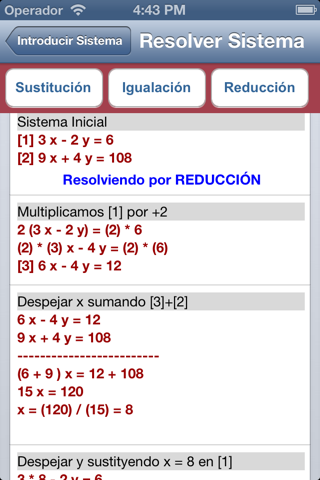
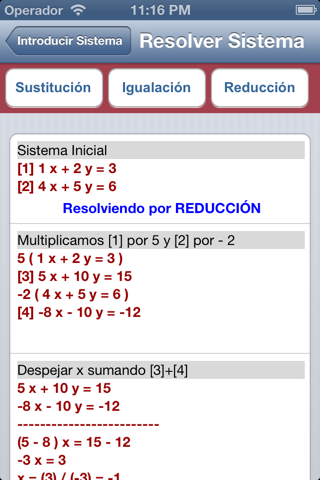
Once entered correctly the system coefficients can see its resolution by the methods of replacement, reduction and equalization . This step by step as if it were made into a book .
In the event that the application is incompatible system implies without any problem.
If its an unknown support system has infinite solutions expressed in terms of a parameter is taken and sets x = t versus t . If it is not possible does the opposite , ie take x = t and put t function .
- In the case of the substitution method first tries to clear the unknown x in the first equation to substitute into the second equation . If this is not possible because the amount of the x coefficient is 0 then try and clear the .
** If you hold the button a menu where you can choose the unknown soy clear first and what equation is shown .
- In the case of the method of matching the unknown x of the two equations is cleared then the resulting expressions equal and solve for y. If you can not isolate x in both equations tries to clear the yy if not possible then it indicates that the system can not be solved by this method.
** If we keep the button pressed a menu where you can decide whether xo is displayed and cleared .
- For the first reduction method which attempts to eliminate the variable and multiplying the first equation by the coefficient of and in the second and multiply the second equation by the coefficient of the opposite and the first . Thus by adding the resulting equations will eliminate the y. If any of these factors be used 0 , you try to delete the analogy x.
Holding the button ** a menu where you first decide whether I want to eliminate x appears.
If a certain system can not be solved by a particular method implies.
Solve all cases of indeterminate compatible systems.